问题：

给定一个无向、连通的树。树中有 n 个标记为 0…n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [a_i, b_i]表示树中的节点 a_i 和 b_i 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sum-of-distances-in-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

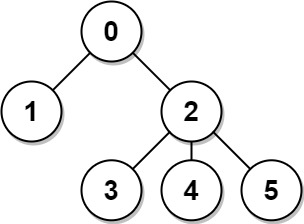
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

    def sumOfDistancesInTree(self, n: int, edges: list[list[int]]) -> list[int]:
        relationTree=[[] for _ in range(n)]
        sonNode=[0]*n
        dp=[0]*n
        result=[0]*n

#我认为这个算法的第一个难点是重建关系，因为是个无向树型图，所以[0,1]中0和1都可以看做是另一方的根。下面这个relationTree就是把这些关系重建。索引为根节点，值为子树。
        for f,s in edges:
            relationTree[f].append(s)
            relationTree[s].append(f)

        def dfs0(root:int, father:int):
            #sonNode[i]保存着i节点有多少个子节点
            sonNode[root]=1
            #dp[i]保存着i节点的子节点到i的举例和。计算过程必须用深度优先的方式从最下层的子树开始计算。
            dp[root]=0
            for item in relationTree[root]:
                if item==father:
                    continue
                dfs0(item,root)
                #dfs0函数返回代表当路径已经到了叶子节点，item就是叶子节点，root是叶子节点的父节点。
                dp[root]+=dp[item]+sonNode[item]
                sonNode[root]+=sonNode[item]
        dfs0(0,-1)
        #dfs1的作用是换根，将与原来的根相连接的节点变成新的根，具体的交换过程可以看力扣834号题目的解题部分的动画。
        def dfs1(root:int, father:int):
            #这个方法也是使用深度优先算法，因为不想对每个节点重新计算一次，本函数是通过使用dfs0的结果"sonNode"和"dp"来生成以其它节点为根时的结果。因为之前已经把0节点为根时的结果计算出来了，所以保存该值到result[root]中
            result[root]=dp[root]
            for item in relationTree[root]:
                if item==father:
                    continue
               #保存当前的值，因为修改过后还要恢复，因为要保持0为根时的所有数据，其它的值都是根据它生成的。
                pd,pn = dp[root],sonNode[root]
                sd,sn = dp[item],sonNode[item]
                dp[root] -= (dp[item]+sonNode[item])
                sonNode[root]-=sonNode[item]
                dp[item]+=dp[root]+sonNode[root]
                sonNode[item]=n
                dfs1(item,root)
                dp[root],sonNode[root] = pd,pn
                dp[item],sonNode[item] = sd,sn

        dfs1(0,-1)

        return result